Präzise Satellitenbahnmodellierung am Beispiel der neuen SWARM-Mission
| Led by: | Prof. Dr.-Ing. Jakob Flury, Dr.-Ing. Akbar Shabanloui, Dr.-Ing. Majid Naeimi, Dr.-Ing. Manuel Schilling |
| Team: | Peter Alpers, Mahsa Bashi, Igor Koch, Damian Kröhnert |
| Year: | 2015 |
| Duration: | WiSe 2015 - SoSe 2016 |
| Is Finished: | yes |




Aktuell werden Satelliten in vielen wissenschaftlichen Disziplinen verwendet. Besonders bei der Bestimmung des Erdschwerefeldes ist es wichtig, den Satellitenorbit präzise zu kennen. In diesem Projektseminar wurde eine Software zur Modellierung und numerischen Integration von LEO-Bahnen in MATLAB implementiert und anhand eines Beispielsorbits der ESA-Mission „Swarm“ getestet.
Eine sehr genaue Modellierung der Satellitenbahn ist durch ein rein analytisches Verfahren nicht mehr möglich. Jedoch existieren numerische Verfahren, welche es erlauben, bei bekannter Position und Geschwindigkeit des Satelliten zu einem definierten Zeitpunkt, zukünftige Positionen und Geschwindigkeiten des Satelliten zu bestimmen. Diese Verfahren werden als numerische Integratoren bezeichnet und benötigen die Kenntnis aller auf den Satelliten wirkender gravitativer und nicht-gravitativer Störbeschleunigungen.
Die größte auf den Satelliten wirkende gravitative Beschleunigung wird durch das Erdschwerefeld hervorgerufen. Im Rahmen dieser Arbeit wurden die Erdschwerefeldmodelle GGM03S, GGM05S und GGM05G verwendet. Die vom Erdschwerefeld hervorgerufene Beschleunigung beträgt 99,99% der Gesamtbeschleunigung. Konkretisiert man diese Gesamtbeschleunigung weiter auf den homogenen Teil, kann man feststellen, dass 99% der Gesamtbeschleunigung durch diesen Anteil hervorgerufen werden. Ein weiterer Beschleunigungseffekt entsteht durch den Einfluss von Drittkörpern. Im Rahmen dieser Arbeit wurde die Auswirkung der Himmelskörper Sonne, Mond, Venus und Jupiter auf den Satelliten berechnet. Die dazu benötigten Positionen der Himmelskörper wurden mit Hilfe der Polynomkoeffizienten des Jet Propulsion Laboratory (JPL) der National Aeronautics and Space Administration (NASA) bestimmt. Indirekte gravitative Beschleunigungen entstehen durch die Gezeiten der festen Erde, welche aufgrund ihrer zu erwartenden Größe nur in den niedrigen Graden n=2 bis n=4 bestimmt werden müssen. Ein weiterer Schritt ist die Modellierung der Ozeangezeiten, welche sich aus der direkten und indirekten Gravitationsänderungen zusammensetzen. Hierfür wurde das Empirical Ocean Tide Model 11a (EOT11a) bis Grad und Ordnung 120 verwendet. Die Berechnung der Polgezeiten der festen Erde und der Ozeanpolgezeiten wurden nach den IERS Conventions umgesetzt. Weitere Betrachtung in dieser Arbeit fanden die relativistischen Effekte des Schwarzschild-Terms, der Lense-Thirring-Präzession und der Geodätischen Präzession. Diese Effekte berücksichtigen die Krümmung der Raumzeit durch das statische und rotierende Gravitationsfeld der Erde, sowie die Berücksichtigung der Präzession durch die statische Masse.
Im Fokus der nicht-gravitativen Effekte stand die Modellierung der atmosphärischen Reibung, des direkten Strahlungsdrucks der Sonne durch den Impuls auf den Satelliten auftreffender Photonen, sowie der Einfluss von der Erde reflektierter kurzwelliger (Albedo) und emittierter langwelliger Strahlung (Infrarot).
Die atmosphärische Reibung stellt den größten Anteil der nicht-gravitativen Beschleunigung eines LEO dar. Für die Bestimmung der atmosphärischen Zusammensetzung und somit der Dichte wurde das Modell NRLMSISE-00 verwendet. Der Einfluss der Sonnenaktivität auf die Dichte wurde durch die Verwendung solarer und geomagnetischer Indizes modelliert. Die Geschwindigkeit des Satelliten wurde relativ zu den Bewegungen der Atmosphäre bestimmt. Hierfür wurde das Windmodell HWM07 verwendet. Die für die atmosphärische Reibung effektive Fläche wurde mit Hilfe eines Makro-Modells bestimmt, wobei für die Bestimmung der Satelliten-Attitude Quaternionen verwendet wurden.
Für die Berücksichtigung des direkten Strahlungsdrucks der Sonne sowie des Effektes der kurzwelligen und langwelligen Strahlung der Erde standen Reflektionskoeffizienten der einzelnen Panel des Makro-Modells zur Verfügung. Der Einfluss des direkten Strahlungsdrucks der Sonne wurde als Summe über alle beschienenen Satellitenflächen bestimmt. Für die Berücksichtigung der konkreten Lichtverhältnisse wurde ein konisches Schattenmodell mit drei Regionen (Licht, Halbschatten, Schatten) verwendet.
Der Effekt durch Albedo und infrarote Strahlung wurde ebenfalls als Summe über alle Panel des Makro-Modells gebildet, wobei im Gegensatz zum direkten Strahlungsdruck der Sonne die Erde nicht als eine Strahlungsquelle definiert wurde, sondern wegen der geringen Distanz zum Satelliten in 64800 Erdelemente (1°x1°-Gitter) eingeteilt wurde. Für die Berechnung des Strahlugsdrucks der einzelnen Erdelemente wurden die Flux-Werte des Clouds and the Earth’s Radiant Energy System (CERES) verwendet.
Es wurden mehrere numerische Integratoren implementiert. Der Runge-Kutta-Integrator verwendet das Einzelschrittverfahren und wurde in der Ordnung 4 und 13 umgesetzt. Als Mehrschritt-Integrator wurde der Adams-Bashforth-Moulton-Integrator der Ordnung 4 implementiert. Das bereitgestellte Softwarepaket beinhaltet außerdem den Adams-Bashforth-Integrator. Es konnte aufgezeigt werden, dass die Abweichungen zwischen den einzelnen Integratoren gering sind und bei gleicher Parameterwahl um mehrere Größenordnungen unterhalb des Positionsfehlers sind. Die einzelnen Verfahren unterscheiden sich somit vor allem in der Laufzeit der numerischen Intergration. Hierbei ist der Adams-Bashforth-Moulton-Integrator zu empfehlen.
Aufbauend auf den hier vorgestellten Effekten wurde mit Hilfe der implementierten Software die Integration mit einer Schrittweite von einer Sekunde beispielsweise für einen 90-minütigen Swarm-Orbit, was ungefähr einem Umlauf eines LEO-Satelliten um die Erde entspricht, durchgeführt. Durch ein sukzessives Anbringen von Effekten und einem Vergleich zum bekannten Sollorbit kann der Einfluss der einzelnen Effekte auf die Genauigkeit der Modellierung aufgezeigt werden. Nimmt man bei der numerischen Bahnintegration an, dass die Erde radialsymmetrisch aufgebaut ist und ein homogenes Schwerefeld besitzt, so bekommt man nach 90 Minuten eine Abweichung von etwa 26 km. Ein bis zum Grad und Ordnung 2 entwickeltes Erdschwerefeld (hier GGM05S), welches vor allem die Erdabplattung berücksichtigt, bringt eine enorme Verbesserung gegenüber der Betrachtung eines homogenen Schwerefeldes. Mit Grad und Ordnung 2 sinkt der Positionsfehler auf 200 m. Mit einer höheren Entwicklung des Erdschwerefeldes wird der Positionsfehler kleiner, wobei die kleineren Ordnungen für den größten Anteil an der Verbesserung beitragen. Entwickelt man das Schwerefeld bis zum maximalen Grad und Ordnung 180, so sinkt der Positionsfehler auf 15 m. Betrachtet man eine ein Zeitintervall von 10 Minuten, was für einige Anwendungen von Interesse ist, so sinkt der Positionsfehler bei Berücksichtigung des voll entwickelten Schwerefeldes auf etwa einen halben Meter.
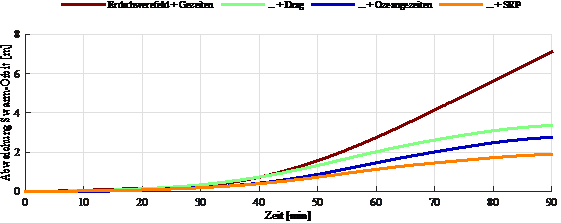
Als weiteren Effekt wurden, zusätzlich zum voll entwickelten Schwerefeld, die direkten Gezeiten der Himmelskörper Sonne, Mond, Jupiter und Venus angebracht. Diese senken den Positionsfehler nach einer 90-minütigen Integration auf etwa 10 m. An dieser Verbesserung hat der Mond wegen seiner Nähe den größten Anteil. Führt man in die Modellierung die Gezeiten der festen Erde als weiteren Effekt ein, so sinkt die Abweichung zum Sollorbit sogar auf 7,1 m (siehe Abb. 1).
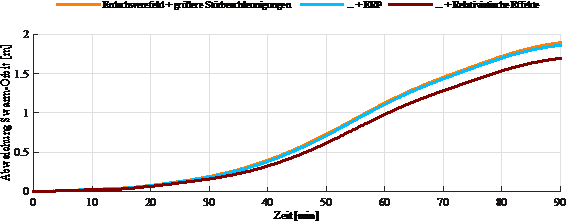
Weitere Effekte führen zu kleinskaligen Verbesserungen. Das Anbringen der atmosphärischen Reibung als nächstgrößten Effekt und größten nicht-gravitativen Effekt bringt eine weitere enorme Verbesserung. Der Positionsfehler sinkt auf 3,4 m. Die zusätzliche Berücksichtigung der Ozeangezeiten senkt die Abweichung zum Sollorbit um weitere 0,6 m auf 2,8 m. Nach der Einführung des direkten Strahlungsdrucks der Sonne beträgt die Abweichung 1,9 m.
Weitere berücksichtigte Effekte Albedo und Infrarotstrahlung (in der Abbildung 2 als ERP zusammengefasst), die relativistischen Effekte, Polgezeiten und Ozeanpolgezeiten können den Positionsfehler minimal senken. Die Abweichung bei Berücksichtigung dller implementierter Effekte beträgt nach 90 Minuten 1,7 m. Der Einfluss der Pol- und Ozenapolgezeiten ist so minimal, dass er in Abbildung 2 nicht dargestellt ist.
Nichtsdestotrotz kann das Ergebnis verbessert werden. So müssen vor allem bei den nicht-gravitativen Beschleunigungen viele Modelle verwendet werden, welche eine gewisse Unsicherheit tragen. So konnte z.B. bei einem Vergleich der atmosphärischen Modelle NRLMSISE-00 und DTM2013 aufgezeigt werden, dass die Abweichung der resultierenden atmosphärischen Dichte über 20% betragen kann. Des Weiteten könnte ein ungenaues Makro-Modell des Satelliten Unsicherheiten einführen, welche größer sind als die Größenordnung einiger kleinerer Effekte. Zusätzlich berücksichtigt das konische Schattenmodell einige physikalische Effekte wie die Refraktion und Lichtstreuung nicht. Durch das implementierten des für die atmosphärische Reibung notwendigen Drag-Koeffizienten als variierenden Faktor können weitere Genauigkeitssteigerungen erwartet werden. Durch die Berücksichtigung der zeitlichen Variation des Erdschwerefeldes, so z.B. durch die Verwendung von GRACE-Monatslösungen, kann der Positionsfehler noch weiter gesenkt werden.
Insgesamt konnte nach einer 90-minütigen Integration eine Abweichung zum Sollorbit von unter 2 m erreicht werden. Nach 10 Minuten beträgt diese sogar 2 cm. Führt man sich vor Augen, dass der Satellit eine Geschwindigkeit von etwa 8 km/s hat und während eines Umlaufs etwa 43000 km zurücklegt, so wird deutlich, dass diese Modellierungsergebnisse die Bahn präzise beschreiben.




