Globales Schwerefeld mittels GRACE High-Low-Satellite-to-Satellite-Tracking / Beschleunigungsansatz
| Leitung: | Prof. Dr.-Ing. Jakob Flury, Dr.-Ing. Akbar Shabanloui, Dr.-Ing. Majid Naeimi, M.Sc. Christoph Wallat |
| E-Mail: | shabanloui@ife.uni-hannover.de |
| Jahr: | 2016 |
| Laufzeit: | WiSe 2016 - SoSe 2017 |
| Ist abgeschlossen: | ja |
Ziel des Projektes
Ziel des Projektes
Die Modellierung des Schwerefeldes gehört zu den zentralen Aufgaben der physikalischen Geodäsie. Mit einem präzisen Schwerefeldmodell können beispielsweise Prozesse wie die postglaziale Landhebung, der Meeresspiegelanstieg oder Eismassenverluste global und quantitativ erfasst werden. Mehrere Satellitenmissionen hatten daher zum Ziel, die Modellierung eines globalen Schwerefelds zu ermöglichen. Darunter fällt auch die GRACE (Gravity Recovery And Climate Experiment) Mission. Sie besteht aus zwei niedrig fliegenden Satelliten, die im Jahr 2002 gestartet wurden und heute noch immer Messungen durchführen. Die Satelliten kreisen in rund 450 km über der Erdoberfläche in einem polaren Orbit. Sie scheinen sich in einem Abstand von rund 250 km zu verfolgen. Der Sinn und Zweck darin besteht, dass so ein Mikrowelleninterferometer eingesetzt werden kann und der Abstand respektive die Relativgeschwindigkeit zwischen den beiden Satelliten, welche sich in Abhängigkeit vom Schwerefeld ändert, auf rund zehn Mikrometer genau gemessen werden kann. Eine weitere Besonderheit der Mission ist, dass monatliche Modelle erstellt werden können. Das Ziel dieses Projektseminars ist die Bestimmung eines Schwerefeldmodells für den Dezember 2008 unter Nutzung der Daten von GRACE. Hier werden jedoch nicht die Abstandsdaten des Interferometers genutzt, sondern die Satelliten werden als freifallende Körper betrachtet. Über die Störbeschleunigungen, die durch das inhomogene Schwerefeld der Erde verursacht werden, kann ein globales Schwerefeldmodell in einem Gauß-Markov-Modell mittels der Methode der kleinesten Quadrate geschätzt werden. Dazu sind präzise Orbits notwendig, die mittels High-Low-SST unter der Nutzung von GPS-Satelliten bestimmt werden können. Sind die Orbits bekannt, so können diese zweimal numerisch differenziert werden und so die auf den Satelliten wirkenden Störbeschleunigungen berechnet werden. Dabei ist es jedoch zwingend notwendig, die anderen gravitativen sowie die nichtgravitativen Beschleunigungen zu subtrahieren.
Durchführung
Das Projekt lässt sich somit in drei Teile aufteilen: Der Berechnung des Orbits, der Störbeschleunigungen sowie die Schätzung eines Schwerefeldmodells.
Um den Orbit zu berechnen, wurden die GPS-Daten genutzt, die mit den Antennen auf den GRACE-Satelliten gewonnen wurden. Ziel war die Berechnung eines kinematischen Orbits, das heißt, dass die Position für jede Epoche mit einer Ausgleichung nach der Methode der kleinsten Quadrate bestimmt wird. Die genutzte Methode war das Precise-Point-Positioning, so wurden Kode- und Phasenbeobachtungen genutzt. Die Orbit- und Uhrdaten der GPS-Satelliten stammten jeweils vom IGS (International GNSS Service) sowie von CODE. Um eine möglichst hohe Präzision und Richtigkeit zu erreichen mussten etliche Fehlerquellen im Rahmen der GPS-Satelliten, der Signalausbreitung sowie im Bereich des Empfangs der von den GPS-Satelliten ausgesandten Mikrowellen. Um den Einfluss der Ionosphäre zu korrigieren wurde beispielsweise die ionosphärenfreie Liniearkombination genutzt. Die anderen Fehlerquellen konnten mithilfe von Modellen sowie Korrekturdaten korrigiert werden. So ließen sich am Ende Orbits berechnen, die eine Richtigkeit von rund einem Dezimeter aufweisen.
Um die auf den GRACE-Satelliten wirkenden gravitativen Störbeschleunigungen zu eliminieren, wurden diese von Drittkörpern ausgelösten Effekte modelliert. Zu diesen Effekten gehören die direkten Tiden, die Gezeiten der festen Erde, die Ozeangezeiten, und die Pol- und Ozeanpolgezeiten. Auch die nichtgravitativen Störbeschleunigungen wurden modelliert, jedoch eher zum Verständnis dieser Effekte. Dazu gehören der Atmosphärenwiderstand, der Strahlungsdruck der Sonne sowie die Erdalbedo. Diese Beschleunigungen werden im Akzelerometer des Satelliten gemessen. Um diese in zu nutzen, mussten ein Offset und ein Skalierungsfaktor in der späteren Ausgleichung mitgeschätzt werden. Hier wurde pro Achse ein Skalierungsfaktor für die gesamten Beobachtungen eines Monats sowie pro Achse jeweils ein Offset pro Tag geschätzt.
Um aus den Positionsdaten des Satelliten, die für jede Epoche vorliegen, Beschleunigungen zu erhalten, muss numerische differenziert werden. Zunächst wurde der Orbit unter Anwendung von B-Splines geglättet, um die Qualität der Beschleunigungen zu verbessern. Um die Positionen abzuleiten, wurde ein Polynom achten Grades in die Positionsdaten geschätzt. Dieses konnte differenziert werden und damit die Beschleunigungen im Orbit berechnet werden. Von diesen Beschleunigungen können direkt die Störbeschleunigungen abgezogen werden – so sind nur noch die Beschleunigungen des Erdschwerefelds vorhanden. Mithilfe der sphärisch harmonischen Analyse, die ein funktionales Modell zwischen den Beschleunigungen und den sphärisch-harmonischen Koeffizienten des Schwerefelds liefert, können diese Parameter in einem Gauß-Markov-Modell nach der Methode der kleinsten Quadrate geschätzt werden. Da die Orbits der der TU Graz eine höhere Genauigkeit als die hier berechneten aufweisen, wurden diese zur Schwerefeldmodellierung eingesetzt.
Ergebnisse
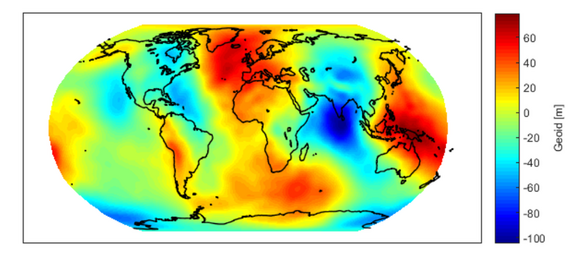
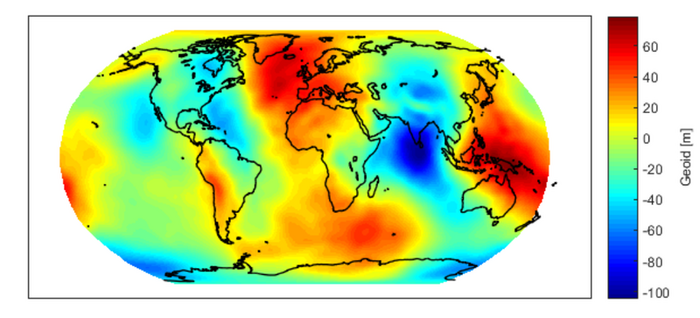
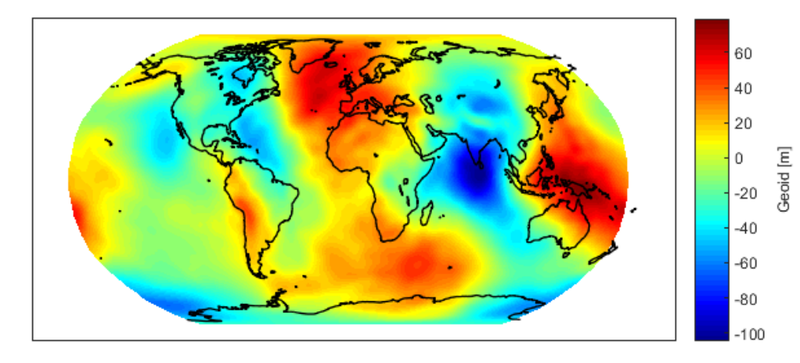
Das Schwerefeldmodell wurde bis Grad 40 geschätzt. Zur Bestimmung höherer Grade müssten die Daten des Mikrowelleninterferometers eingesetzt werden. Die Qualität des Modells wurde sowohl im Ortsraum als auch im Frequenzraum überprüft. Hierzu wurde zunächst das hier berechnete Modell mit dem ITGS Modell von 2008 verglichen. Dabei gibt es Differenzen von bis zu 15 cm, im Mittel liegen diese aber nur bei sieben Zentimetern. Um das Modell auch im Frequenzraum zu überprüfen wurden die Gradvarianzen berechnet, dabei werden die Varianzen, die mithilfe der Ausgleichung bestimmt werden, für jeden Entwicklungsgrad aufsummiert. Durch einen Vergleich dieses Fehlers pro Grad mit den Koeffizienten kann das Signal-zu-Rausch Verhältnis bestimmt werden und auch der maximal sinnvolle zu schätzende Entwicklungsgrad der Koeffizienten ermittelt werden. Sind die Gradvarianz und das Signal gleich groß, so ist bereits keine signifikante Information mehr in den Koeffizienten enthalten. In dem hier berechneten Modell ist das Signal-zu-Rausch Verhältnis bis Grad 17 hoch, dann steigt es und es zeigt ein auffälliges Verhalten, was eventuell auf systematische Effekte hinweisen kann.
Eine Verbesserung könnte erreicht werden, indem die Beschleunigungen mittels einer direkten Ableitung aus den B-Splines gewonnen werden, die bereits zur Glättung des Orbits eingesetzt wurden. Insbesondere Überschwinger, die bei Polynomen auftreten, können so vermieden werden. Um die GPS-Beobachtungen zu verbessern, wäre eine Verwendung von Uhr- und Positionsdaten von derselben Quelle sinnvoll, da diese miteinander korreliert sind.Eine Verbesserung könnte erreicht werden, indem die Beschleunigungen mittels einer direkten Ableitung aus den B-Splines gewonnen werden, die bereits zur Glättung des Orbits eingesetzt wurden. Insbesondere Überschwinger, die bei Polynomen auftreten, können so vermieden werden. Um die GPS-Beobachtungen zu verbessern, wäre eine Verwendung von Uhr- und Positionsdaten von derselben Quelle sinnvoll, da diese miteinander korreliert sind.




